O professor Nelson Carnaval fez uma análise dos conteúdos de Raciocínio Lógico-Matemático que serão cobrados no concurso do Banco do Brasil. Dividimos a análise em três partes e em cada uma delas tem questões resolvidas para ilustrar como os assuntos podem ser cobrados pela banca Cesgranrio.
Análise da primeira parte:
Números inteiros e racionais: operações (adição, subtração, multiplicação, divisão, potenciação); expressões numéricas; múltiplos e divisores de números naturais; problemas. Frações e operações com frações.
A primeira parte do programa de matemática refere-se ao conteúdo de aritmética, ou seja, problemas com as quatro operações. É necessário conhecer o conjunto dos números naturais, inteiros, racionais e irracionais. Saber quais são os elementos marcantes de cada conjunto bem como saber realizar operações com eles. Vale salientar que as questões com esses conjuntos podem ser teóricas, no sentido de saber se uma operação é ou não fechada nesse conjunto. A cesgranrio é bastante tradicional nessa parte, costuma até cobrar a resolução de determinadas expressões com dízimas infinitas periódicas, por exemplo.
Alguns exemplos básicos podem ser vistos nos problemas a seguir:
01. (CESGRANRIO) Se r é um número racional e m um número irracional, podemos afirmar que:
a) r.m é um número racional
Falso (continua irracional)
b) r.m é um número irracional
Falso (resultado racional)
c) r + m é um número irracional
Verdadeiro (continua irracional)
d) (r + 1)m é um número racional
Falso (continua irracional)
e) m2 é um número racional
Falso (continua irracional)
02. Às 8 horas e 45 minutos de certo dia foi aberta uma torneira, com a finalidade de encher de água um tanque vazio.
Sabe-se que:
– o volume interno do tanque é 2,5 m3;
– a torneira despejou água no tanque a uma vazão constante de 2l /min e só foi fechada quando o tanque estava completamente cheio.
Nessas condições, a torneira foi fechada às
5 horas e 35 minutos do dia seguinte.
4 horas e 50 minutos do dia seguinte.
2 horas e 45 minutos do dia seguinte.
21 horas e 35 minutos do mesmo dia.
19 horas e 50 minutos do mesmo dia.
SOLUÇÃO:
Volume 2,5m3 x 1000 = 2500L
Vazão da torneira: 2l /min. Logo, 2500/2 = 1250 Minutos. Assim, a duração foi 20h e 50 min.
Para achar o término, somamos o tempo gasto ao tempo de início:
Letra A
03. Se numa divisão o divisor é 30, o quociente é 12 e o resto é o maior possível, então o dividendo é:
a) 390
b) 389
c) 381
d) 361
e) 350
SOLUÇÃO:
O maior resto possível de uma divisão é uma unidade a menos que o divisor.
Letra B
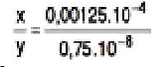
04. Sejam x e y números inteiros e positivos tais que a fração x/y na expressão abaixo é irredutível, ou seja, o máximo divisor comum de x e y é 1. Logo, x + y é igual a
a) 53.
b) 35.
c) 26.
d) 17.
e) 8.
SOLUÇÃO:
Letra A
05. Uma certa porção de líquido foi distribuída igualmente pelos recipientes A, B e C. Posteriormente, os conteúdos de B e C foram repartidos igualmente pelos recipientes A, B, C, D e E. Que fração de porção total ficou contida no recipiente A?
a) 1/3
b)15
c)17/12
d)7/3
e) 7/15
SOLUÇÃO:
Cada um dos recipientes A, B e C tem 1/3 do líquido.
Pegando B e C, ou seja, 2/3 e dividindo para A, B C, D e E, temos: 2/3 : 5 = 2/3 . 1/5 = 2/15.
Logo, o A que já tinha 1/3, recebeu mais 2/15 e ficou com a fração:
Letra E

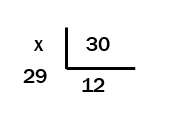

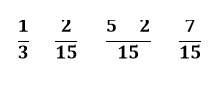



Comentar